type
status
date
slug
summary
tags
category
icon
password
Property
Mar 25, 2025 01:54 AM
URL
6.1 刚性转子的能级
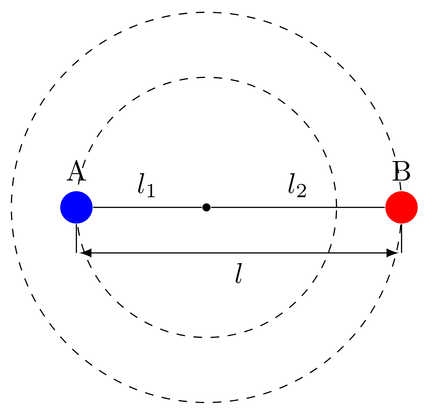
动能:
转动惯量:
用约化质量,可以将转动惯量写成:
角动量:
动能和角动量的关系:
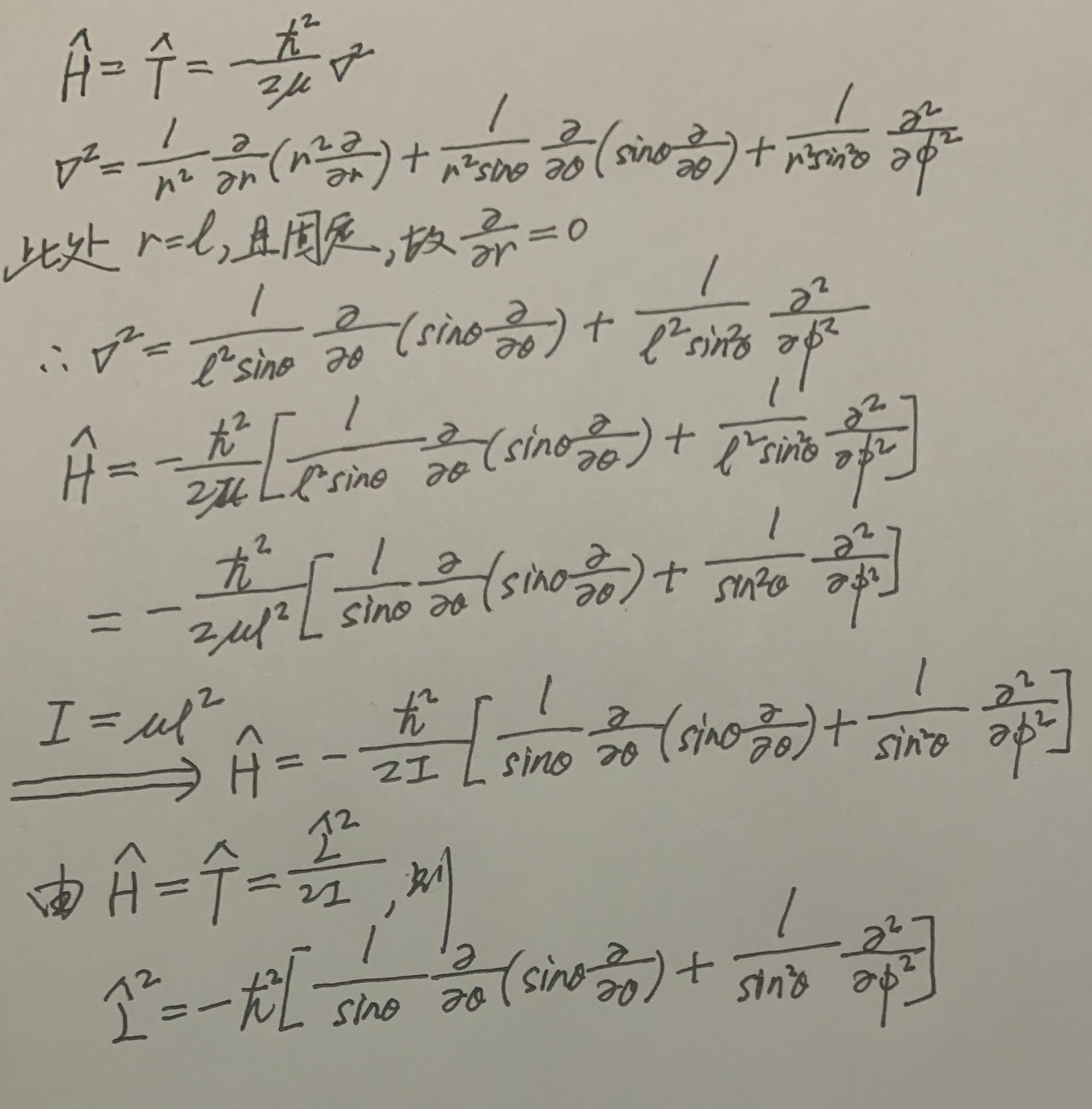



我们最后得到的能量就是:
6.2 刚性转子是旋转双原子的一个模型
刚性转子的选律:

转动光谱不太知名,此外转动能级远低于振动或者电子能级的能量
双原子的刚性转子模型预言了双原子的微波谱由一系列间隔为 或者波数为 的线构成
我们可以根据光谱间隔知道 的值,然后通过 的公式计算出 , 那么我们就能计算出键长
下面是一个典型的例题
【例】为了便于应用,HCI 的微波谱由一系列等间距的谱线组成,谱线之间相隔,计算 HCl 的键长
由公式:
再由
6.3 旋转跃迁伴随着振动跃迁
转动和振动能量的和是如下的公式:
说明
- 振动的贡献大于转动
- 基态时候
如果使用波数表示,那么公式就变成了:
,,
这两个数的数量级是这样的,,也说明了振动的贡献比较大
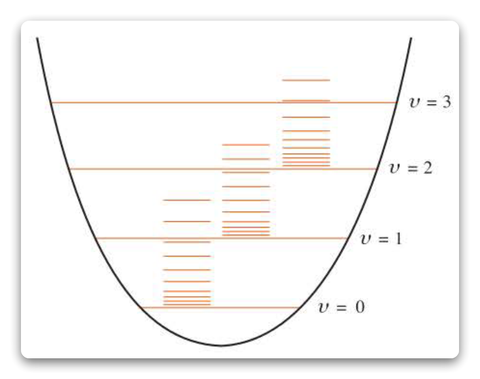
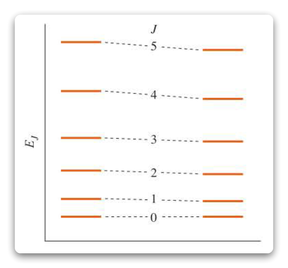
问题:图中的线随着n的增大,为什么会从左往右移动?
在振动-旋转能级图中,x轴表示旋转量子数J,y轴表示能量。在这个图中,我们观察到的是旋转能级与振动能级之间的关系。
对于二原子分子,总能量由振动能量和旋转能量之和组成。随着振动量子数n的增加,分子的振动能量增加。当振动能量增加时,分子的有效转动惯量会发生变化。这会导致旋转能级之间的能量差(即旋转能级的间距)随着n值的增加而变化。
在振动-旋转能级图中,每个振动能级都有一系列与之关联的旋转能级。当我们从低振动能级到高振动能级(即n值增大)时,旋转能级之间的间距会发生变化。这种变化反映了旋转能级与振动能级之间的耦合关系。
因此,当我们说线从左向右移动时,我们实际上是在描述旋转能级与振动能级之间的关系如何随着n值的增加而变化。这并不意味着能量本身在x轴上移动,而是指随着n值的增加,旋转能级之间的间距会发生变化。
当分子吸收红外辐射时,振动跃迁伴随着转动跃迁。刚性转子-谐振子近似中吸收红外辐射的选择规则为:
振动光谱和旋转光谱的耦合可以产生振动-旋转光谱,但要满足它们各自的条件才能观察到这种现象。
在分子振动光谱中,分子的振动能量被激发,导致分子的键长、键角等形状参数发生变化。在分子旋转光谱中,分子的整体旋转受到激发,导致分子的角动量发生变化。在振动-旋转光谱中,振动和旋转运动相互耦合,可以产生新的能级结构和光谱线。
在实际的实验中,我们通常需要满足分子振动和旋转的条件才能观察到振动-旋转光谱。例如,在红外光谱中,我们需要通过改变光谱仪的分辨率来增强分子振动跃迁的信号,并减少旋转跃迁的信号。在微波光谱中,我们需要使用低温和高分辨率的仪器来增强分子旋转跃迁的信号,并减少振动跃迁的信号。
因此,只有当满足分子振动和旋转的条件时,才能观察到振动-旋转光谱。如果只满足其中一种条件,那么我们只会观察到振动光谱或旋转光谱。

P 分支是由于 ,R 分支是由于
[例题] 已知 CN 的键长为 117pm,力常数=1630 N/m,预测转动-振动频率
首先计算他们的约化质量:
然后利用上面的波数公式计算可以计算:
同时:
所以转动-振动频率为
我们仔细观察发现,随着频率的增加, 分支中的线条更加紧密,而 分支中的线条随着频率的减小而变得更远,用上述的计算结果看不出来这个规律,我们需要解决这个问题
6.4 旋转-振动相互作用解释了旋转-振动谱P支和R支线间距不等的原因
重新观察 旋转-振动模型:
随着振幅的增大,我们说 l 也就是双原子分子的间距会略微变大,这是为什么呢,简单的谐振子模型中
并没有包含键长,这里看不出来 l 会随着振幅的增大而增大,我们使用 Morse 模型
- :势能;
- :原子间距离;
- :平衡键能,即原子间距离在平衡位置时的势能;
- : Morse势参数,决定了势能曲线的形状;
- : 平衡距离,即原子间距离在平衡位置时的值
在Morse势模型中,势能随原子间距离的变化呈现出非线性特性。这种非线性特性允许我们更准确地描述分子振动行为,特别是在高振动能级下
通过求解Morse势模型的薛定谔方程,我们可以得到振动能量公式:
其中:
- :振动能量;
- :振动量子数;
- :约化普朗克常数;
- :平衡振动频率;
- :振动频率的一阶修正项,与Morse势的形状有关。
这个公式中包含了振动频率的一阶修正项,使得振动能量与振动量子数之间的关系变得非线性。这个非线性关系允许我们考虑振动能量增加导致原子间距离变大的现象。
Morse势能模型是一个相对简单但更逼真的非简谐振动模型。通过使用这个模型,我们可以更好地解释振动能量增加导致原子间距离变大的现象。当然,还有其他更复杂的模型,如Dunham展开、Rydberg-Klein-Rees(RKR)势能曲线等,可以用于描述分子振动行为。
上面已经解释说明了振动的增加会导致 的增加,与此同时 中含有 ,所以我们可以说 也依赖于振动,也就是 也依赖于 ,所以我们看可以把 改写成 ,最后整理一下公式就可以得到:
这里的 被叫做旋转-振动相互作用
现在我们考虑 n=0 →1 那么就可以得到:
分支:
分支:
在上述的等式中,当,则退化成了
也就是我们开始讨论的 和 分支的公式,由于键长随 的增大而增大, ,因此 分支的线的间隔随 的增大而减小;同理, 分支的线的间隔随 的增大而增大

【例】R和P分支中的谱线通常被标记为导致这些谱线的旋转量子数的初始值。因此,由方程6.41给出的线是R(O),R(I),R(2)......,而由方程6.42给出的线是P(I),P(2)......针对 HI 给定以下数据:
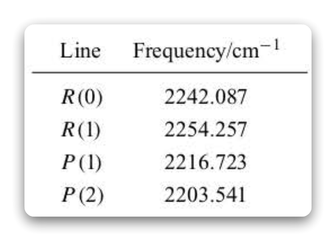
根据以上数据计算 ,
联立上面的四个方程我们可以求解出
6.5 纯转动谱中的线不是等间距的
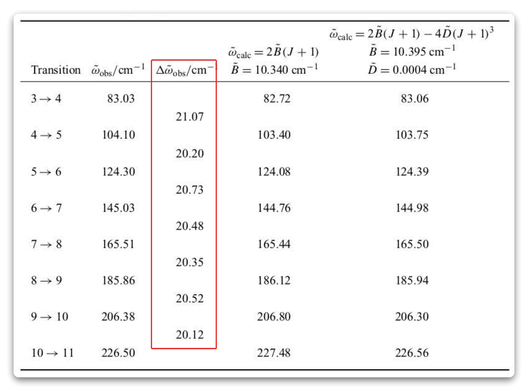
观察这张图的第三列,可以看到频率不是等间距的。。第三列中列出的差异清楚地表明,线条并不像刚性转子近似预测的那样完全等距。这种差异可以通过认识到化学键并不是真正的刚性来解决。随着分子旋转的能量越来越大(增加 J),离心力导致键轻微拉伸。这个小的影响可以用微扰理论(第 8 章)来处理,最终的结果是能量可以写成
这里的 被称为离心畸变常数
当
6.6 刚性转子的波函数称为球谐函数
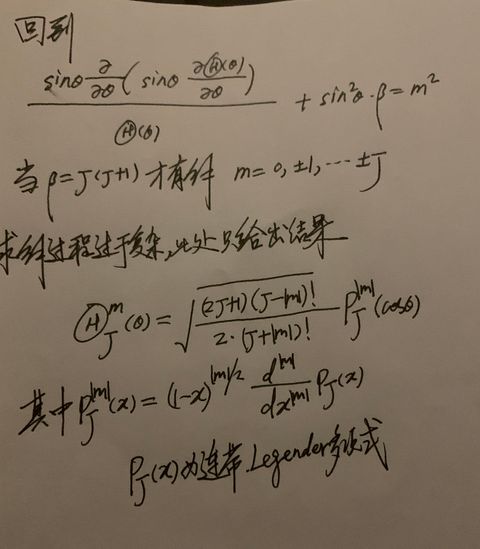
最后我们可以得到下面的结论
6.7 刚性转子的选律是



- 作者:NotionNext
- 链接:https://tangly1024.com/article/qc-6
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。




