type
status
date
slug
summary
tags
category
icon
password
Property
Aug 25, 2023 05:15 PM
URL
写这篇文章是受人邀请写的,然后自己本科的时候看过一篇文章叫做 我为什么喜欢Mathematica ,受这个文章的启发,我也准备写一个和他一样名字的文章,致谢改文章的作者.
Mathematica 是一个非常好用的数学工具,和 Matlab, maple 并称为世界三大数学软件,只可惜 Mathematica 软件在国内并不受待见,如果你真正用过就会知道它的好! 比 Matlab好用很多!
Mathematica 全程应该是 Wolfram Mathematica,国内都简称为 mma ,实际它是一个编程语言,叫 Wolfram 语言我认为更合适,所以我后文就叫它 Wolfram 语言.
1. 界面介绍
1.1 主页面
如图所示就是它的界面,非常的简洁有没有!
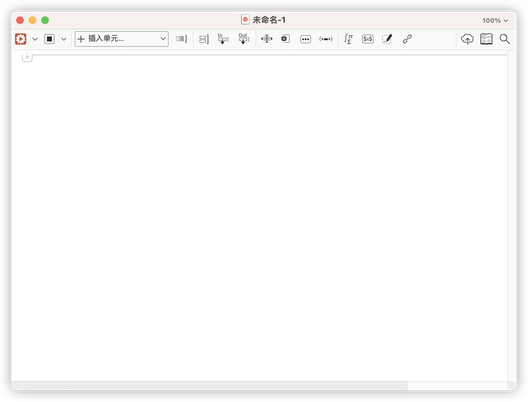
对比一下 Matlab 和 maple 简直就是美到极点!
1.2 排版功能
wolfram 语言内置了各种助手,就算你是啥也不懂的小白,对照这些排版助手,也能整出各种数学公式,可以说 Wolfram 语言就是为了数学而生的
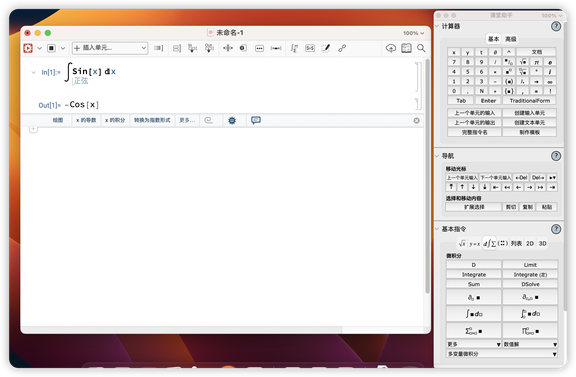
Wolfram 语言中还能设置标题,章节等各种你想要的排版功能.
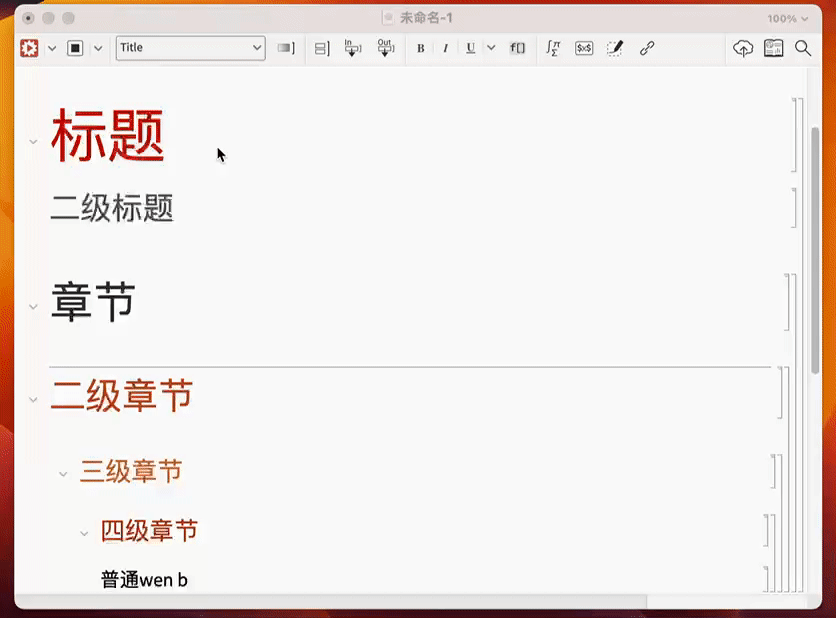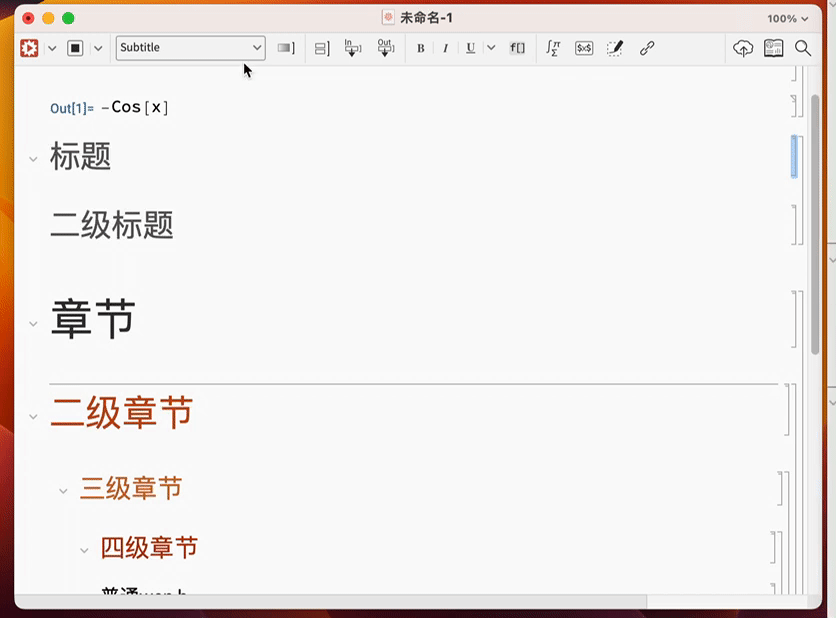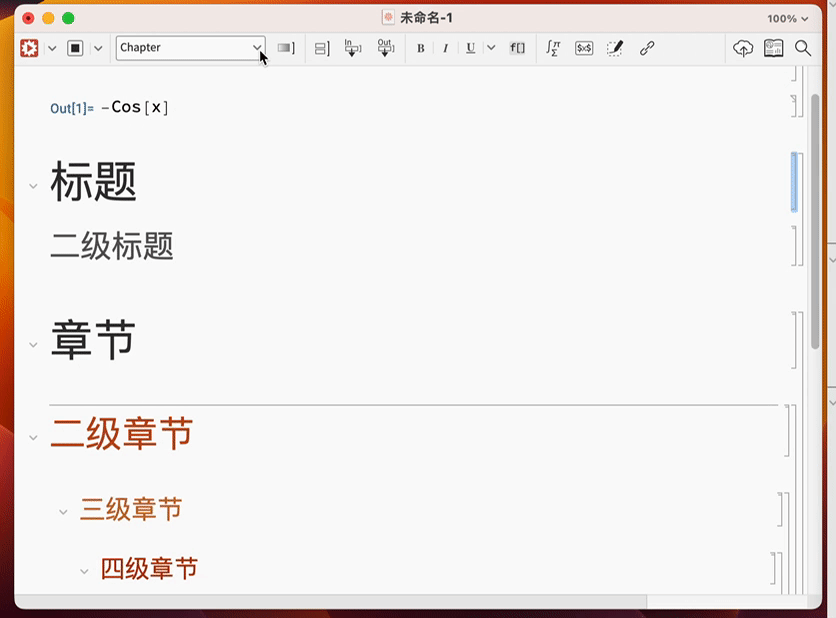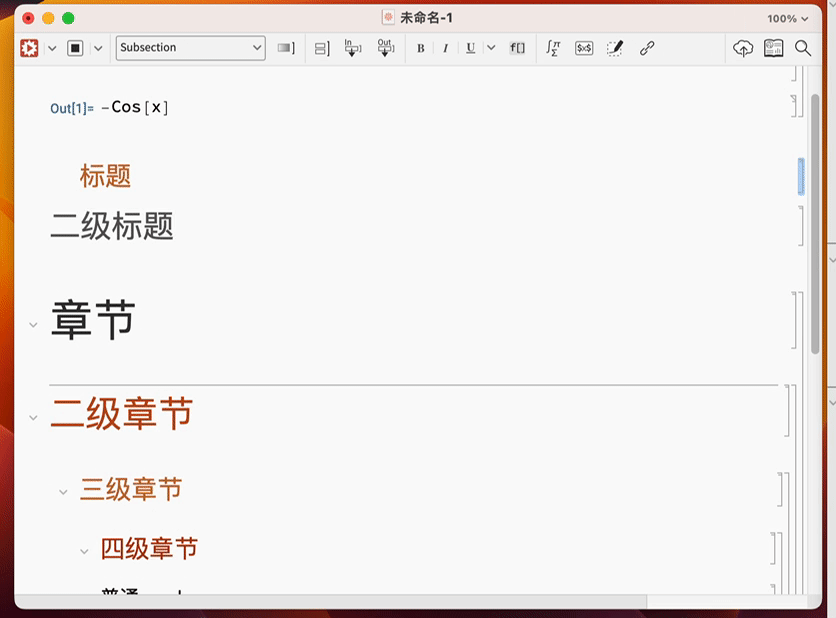
通过调节这些设置,通过熟练掌握,你可以制作出精美的图书:


还能制作幻灯片,注意这个是可以动的幻灯片,而且里面的结果都是可以运行的!别人都用 ppt ,你用 Wolfram 语言,是不是逼格很高!
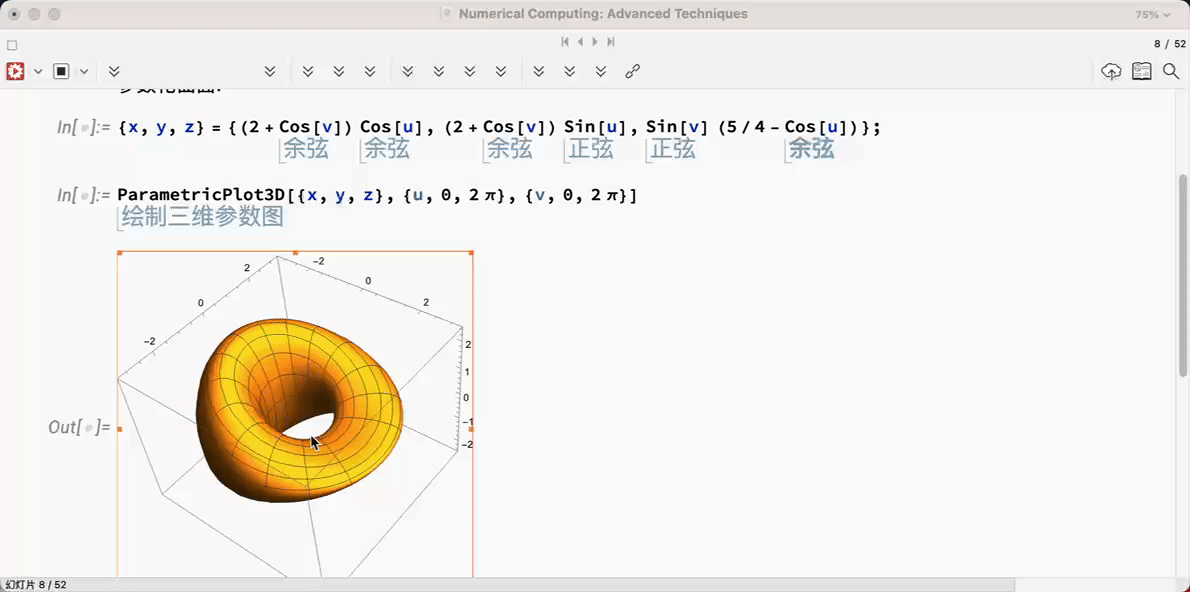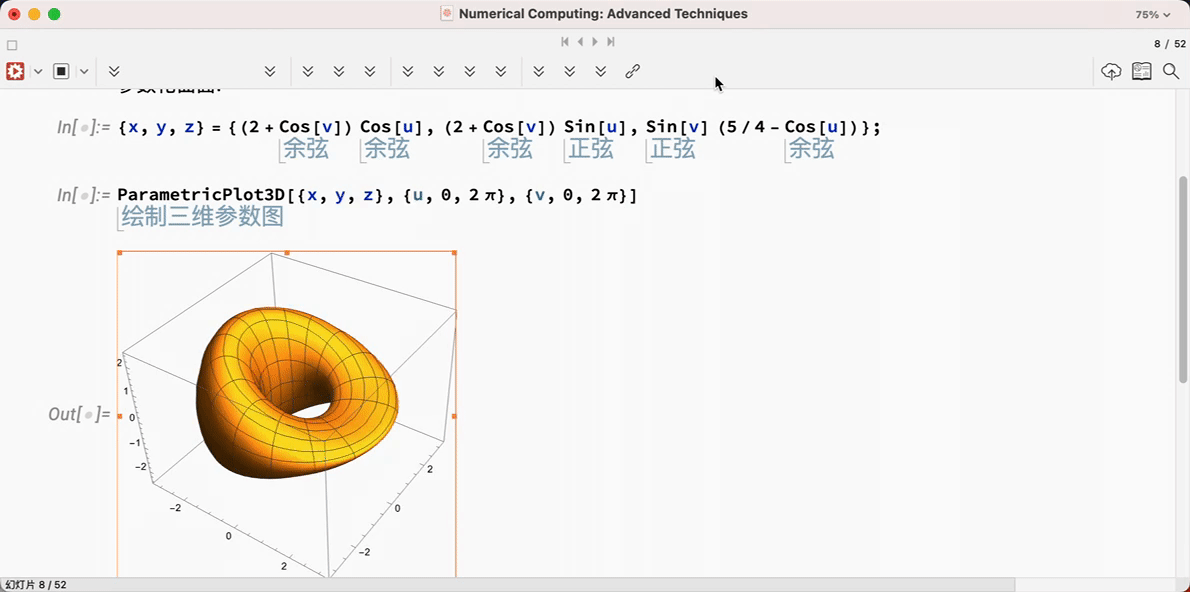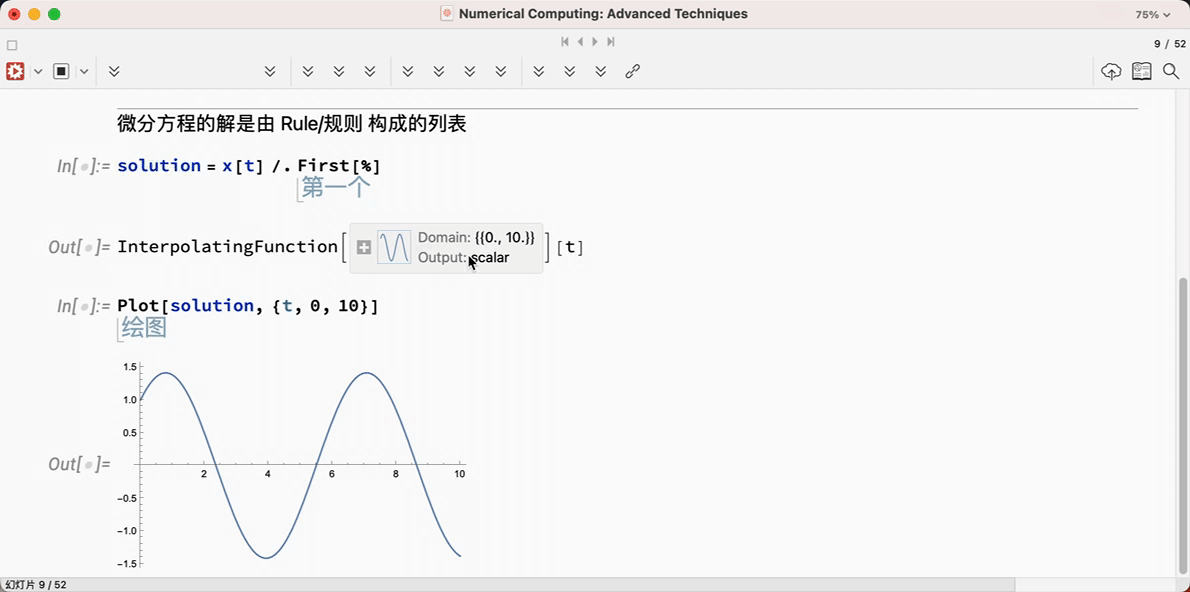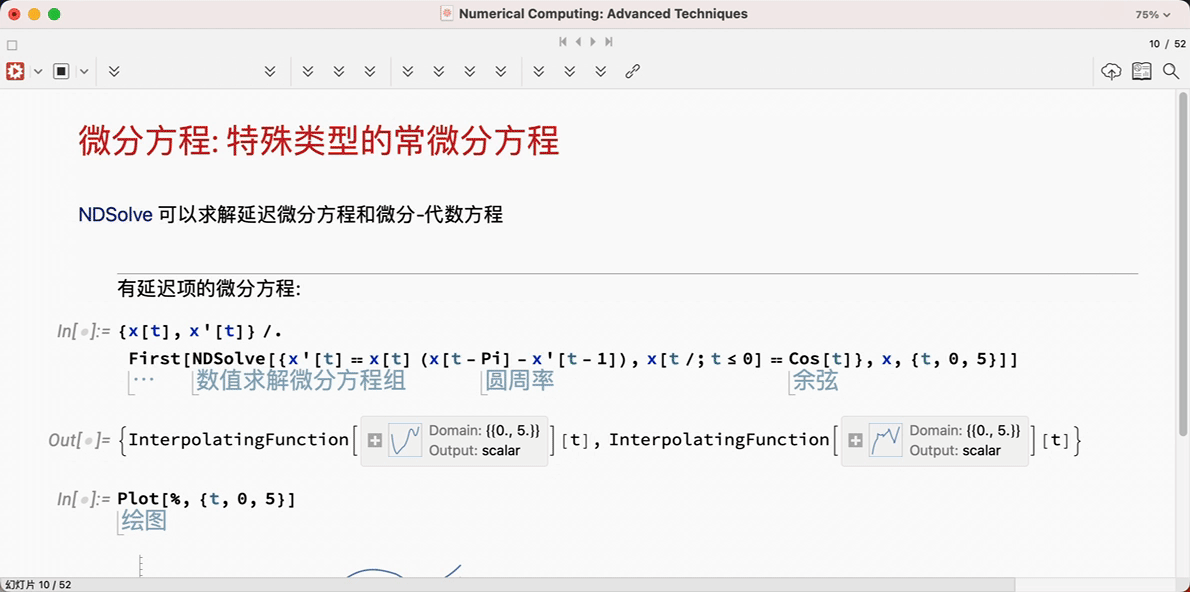
1.3 帮助文档
想一想你学很多编程语言的时候,是不是很多资料都得去百度或者谷歌查?因为大多数编程语言都是外国人开发的,都是英文的文档,像 Matlab,maple 自带的帮助文档就是英文的非常不方便,来看看 Wolfram 语言的!
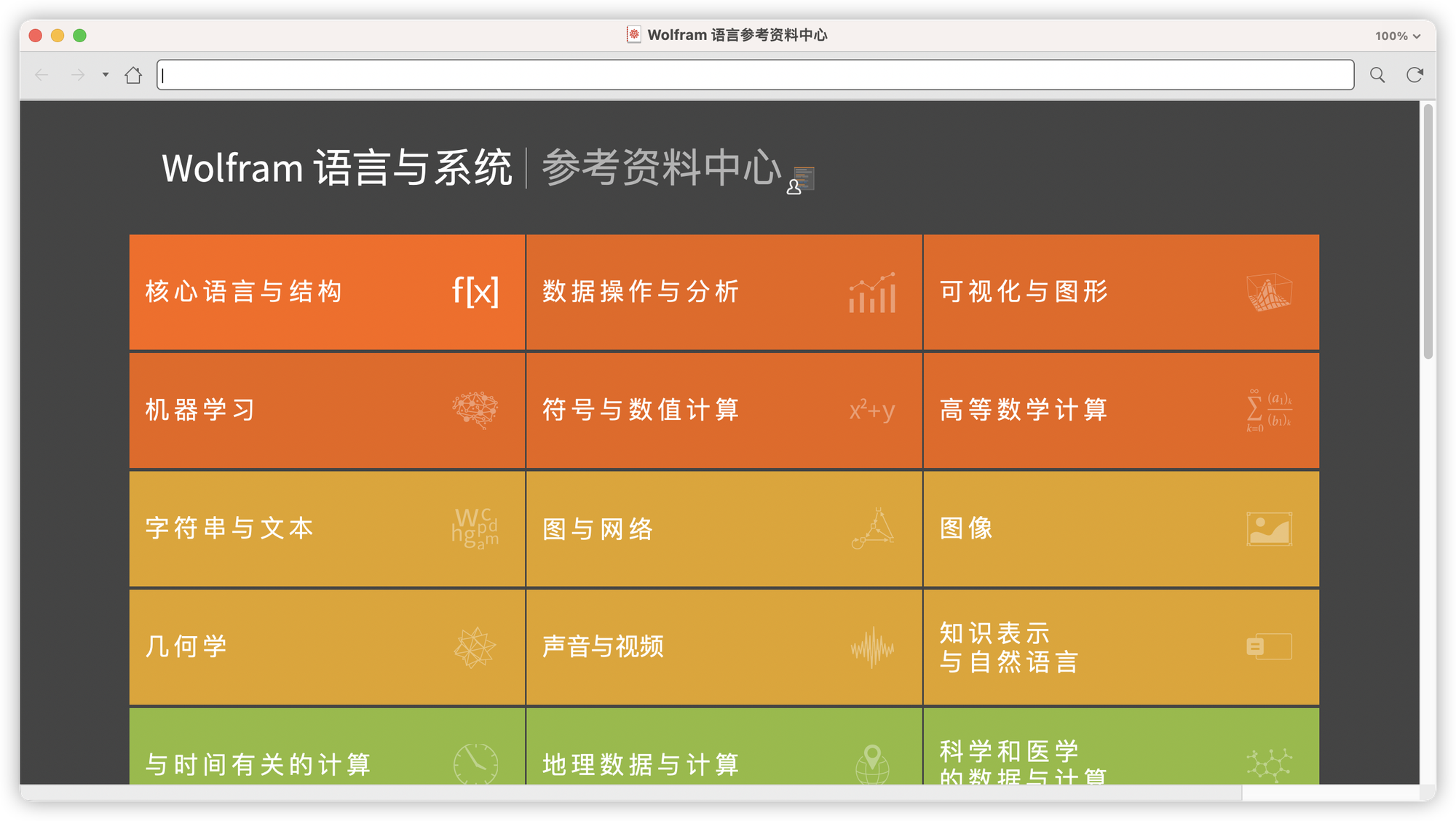
看到没,你想学什么直接去查,而且是中文的,帮助文档都是可以随便运行的,关键是中文!
举例来说你想画图,直接查就行了!各种例子都有,简直就是个百科全书,应有经有!
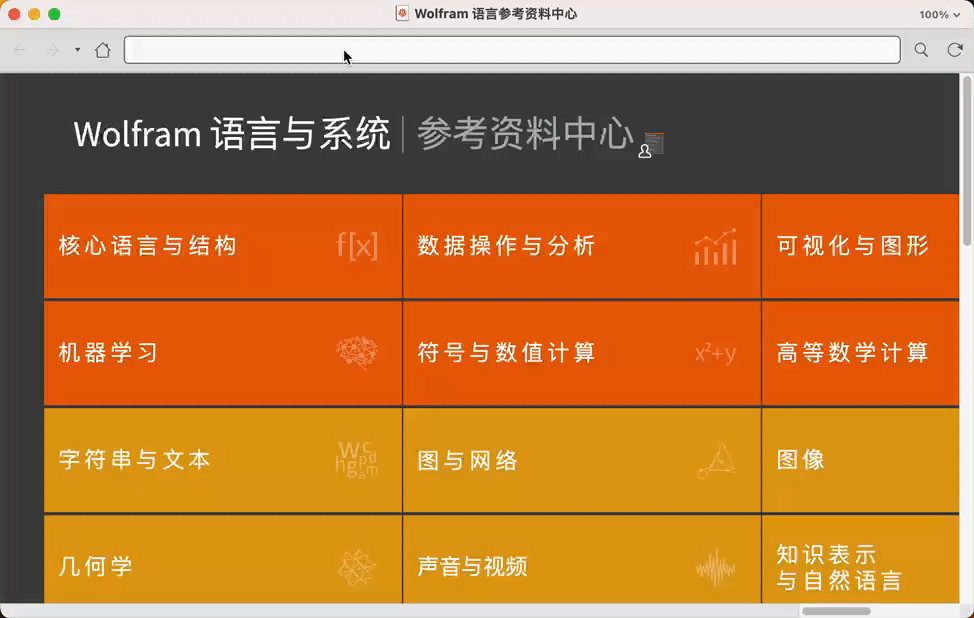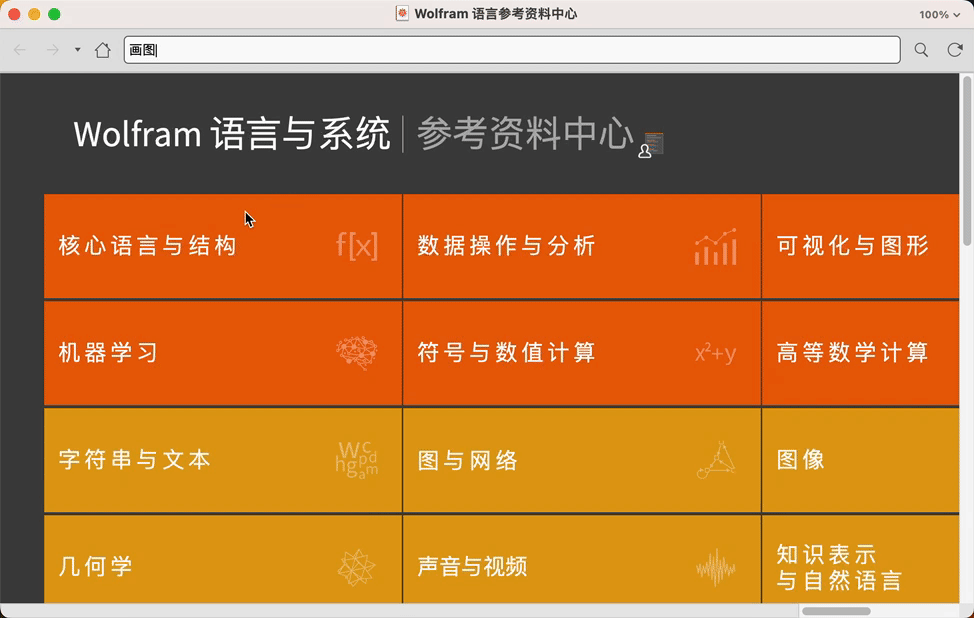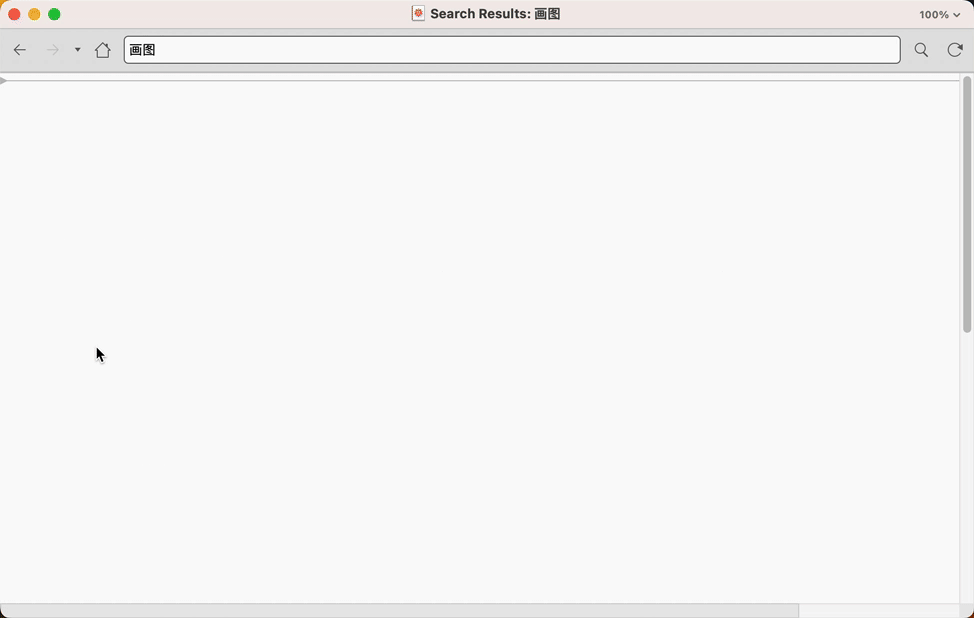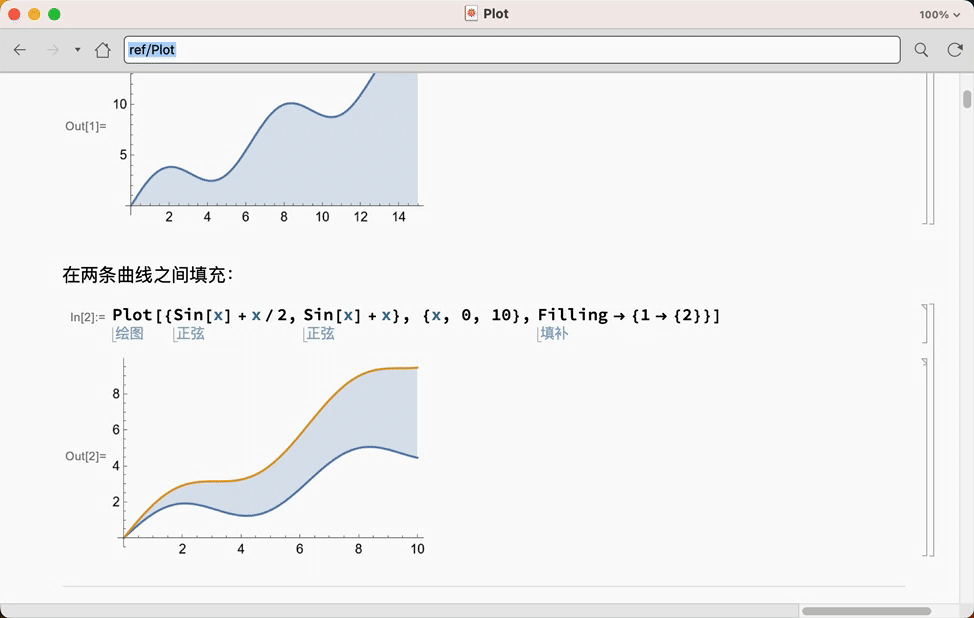
学 Wolfram 语言的人经常讲,帮助文档就是最好的学习资料!
2. 编程能力
说了这么多我们似乎还没进入正题,Wolfram 语言的强大之处还在于它的编程,以及学习的友好度.
2.1 代码提示
代码提示? 有些人可能会感觉好笑,几乎所有的编程语言都有代码提示,但是和 wolfram 语言相比就是弟弟
下面的例子中,把关键词 Plot 是绘图, Sin 是正弦, Pi 是圆周率全部告诉你了,你一眼就能看懂
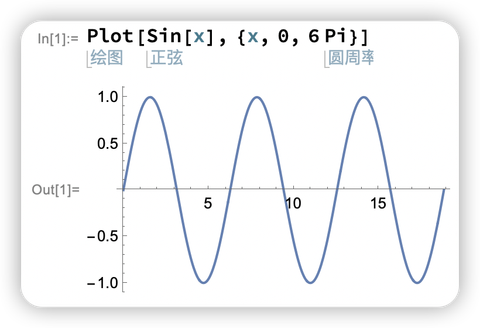
你是不是经常记不住命令?Wolfram 语言来帮助你
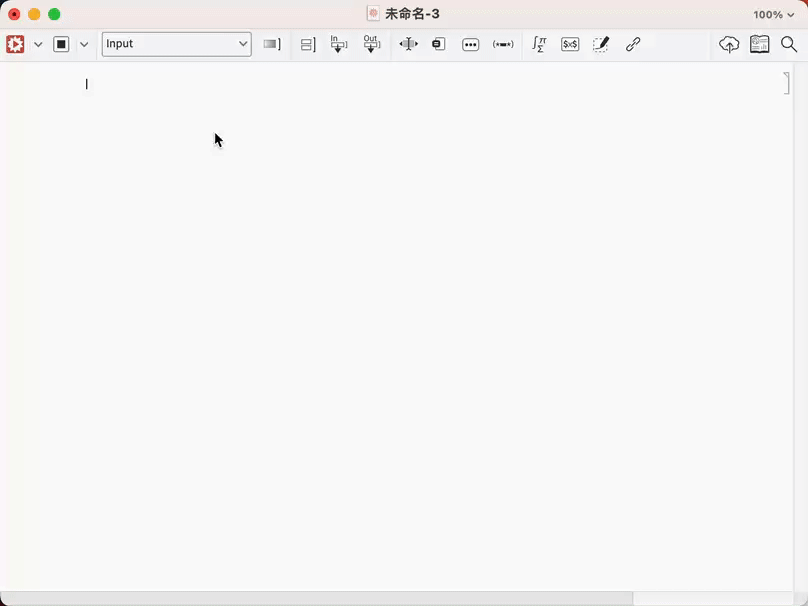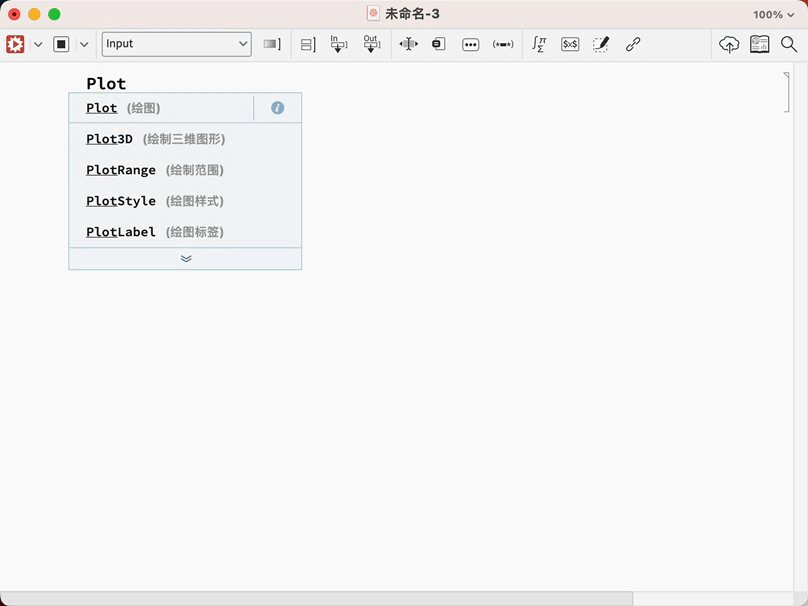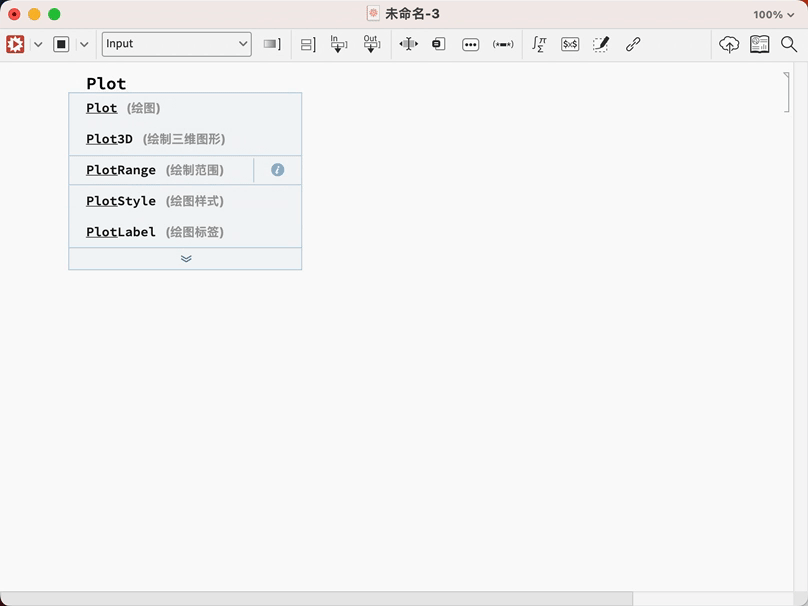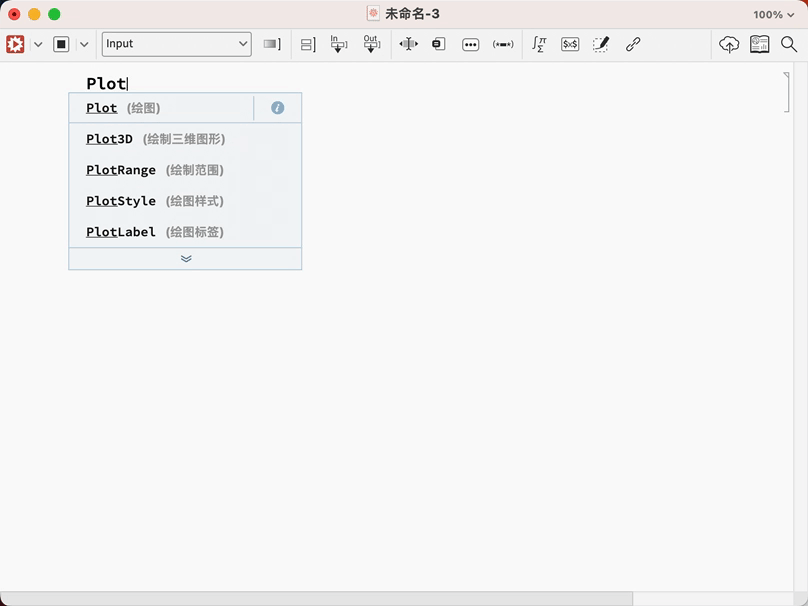
看见了吗?全部都是提示,而且是中文的!我就问牛不牛!
你也许说我命令记不住解决了,我是小白我不知道怎么输入啊,还是可以帮你!
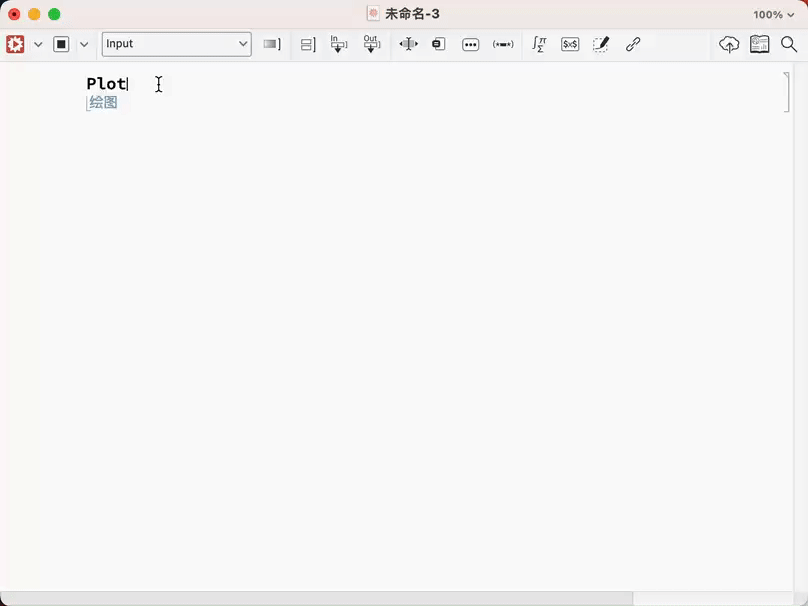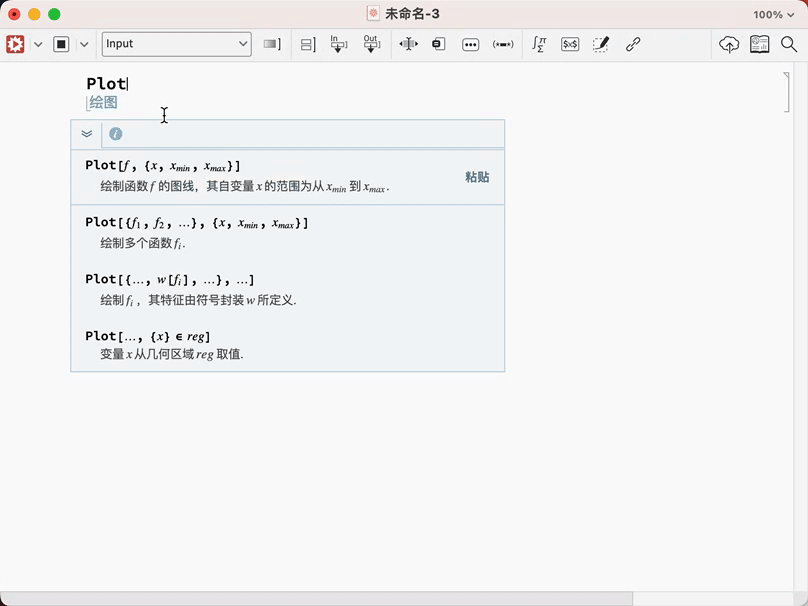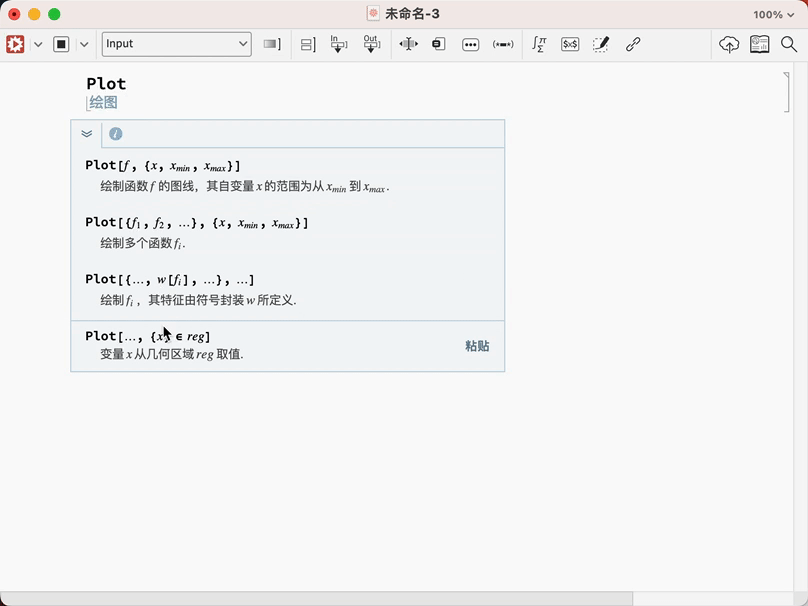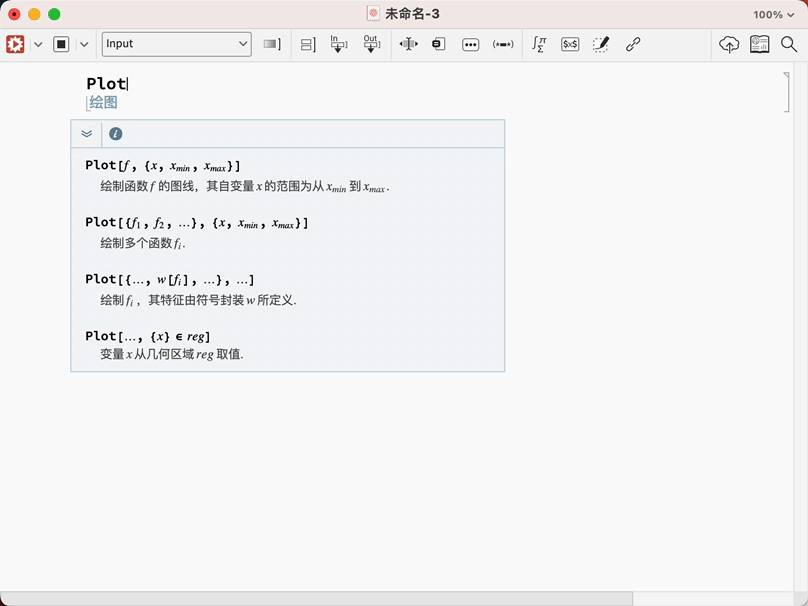
看见了吧,直接告诉你怎么输入,是不是很方便.
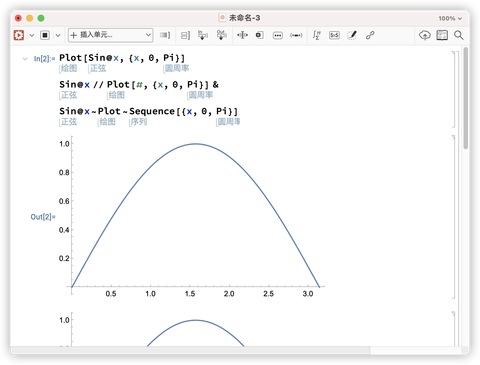
2.2 多种输入形式
看见没有下面的一个绘图程序,可以用三种不同的表现形式来展示,非常灵活的输入
各种函数的简写
你可能看不懂,你只需要知道,通过这些简写的代码,可以将原来几行甚至几十行的代码弄成一行来完成,说到这里就不得不说一下 Wolfram 语言每年举办的 “一行代码” 大赛


上面这些只是冰山一角.
2.3 一切皆表达式
在 Wolfram 语言中所有的东西就是表达式
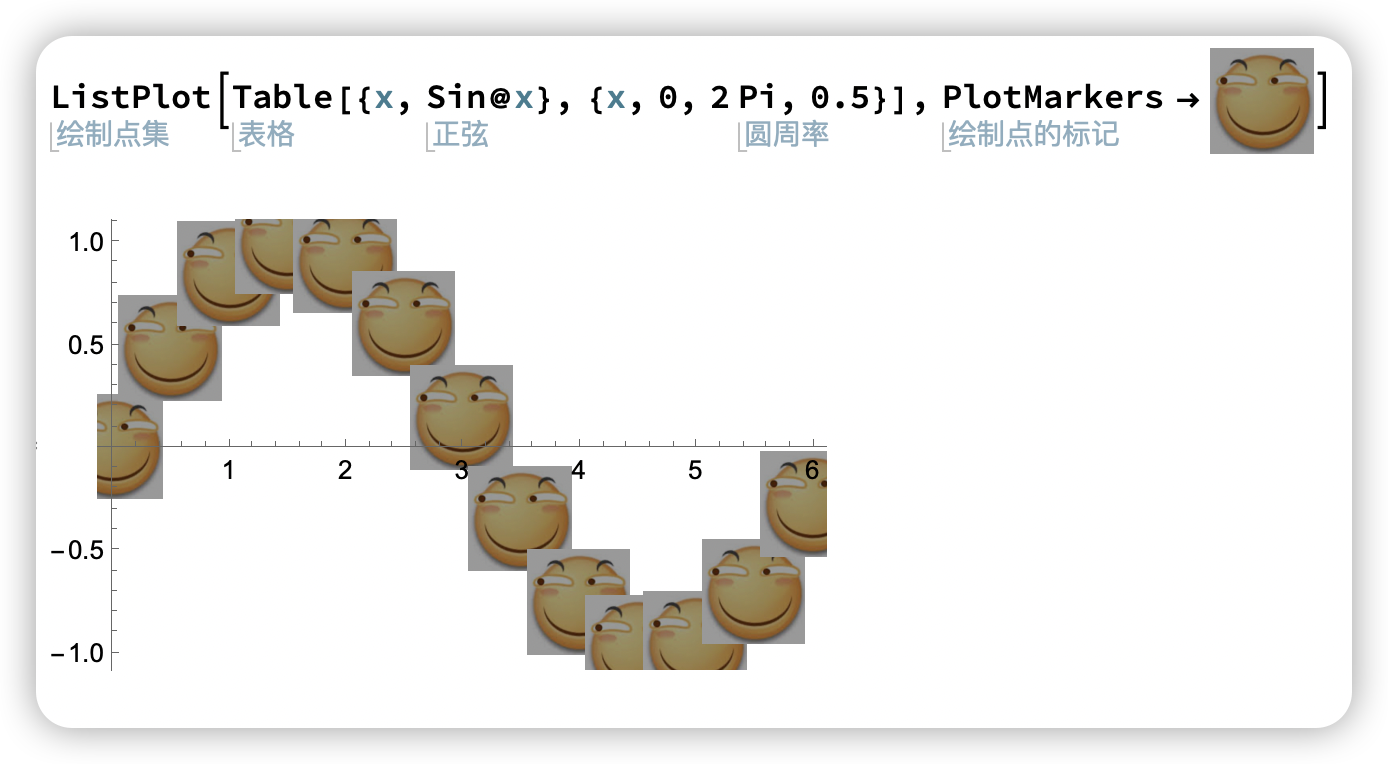
对图片做运算

直接将图中的点替换成滑稽图像
去“码”
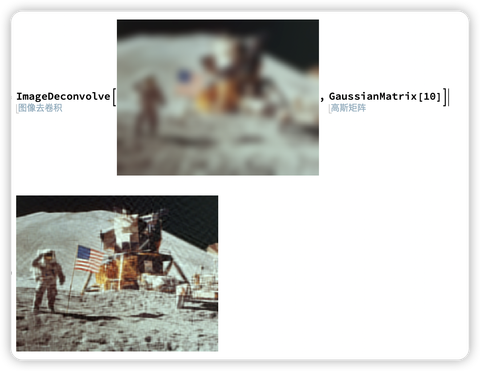
是不是可以….,你懂的(滑稽)…
2.4 强大的绘图能力
下面展示部分绘图
2.4.1 手绘石墨烯
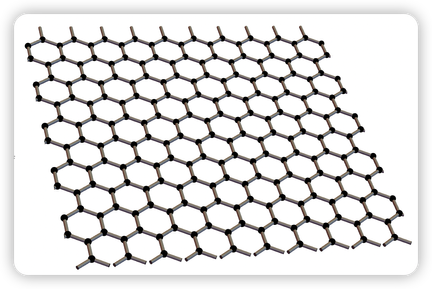
2.4.2 制作同步时钟

2.4.3 制作原子轨道图

2.4.4 手绘元素周期表
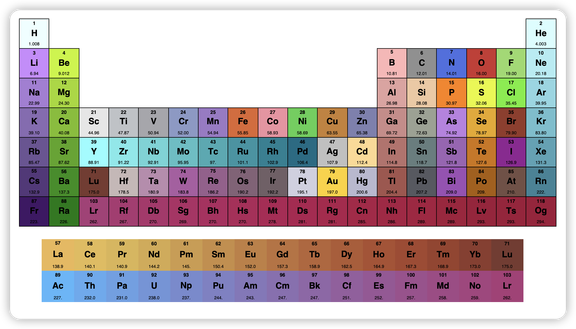
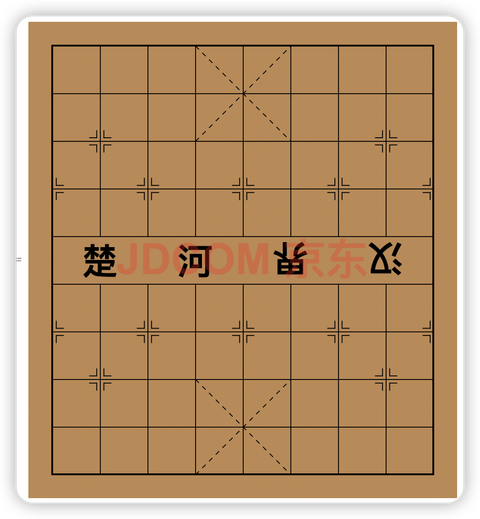
2.4.5 制作象棋棋盘
3. 小结
上面说的只是部分,连 Wolfram 语言 1% 的功能都没说到,模式匹配,规则替换,纯函数等各种牛逼的功能这里都没说,只是多举例图像的例子,会有个更加直观的理解.
- 作者:NotionNext
- 链接:https://tangly1024.com/article/why-mma
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。




