type
status
date
slug
summary
tags
category
icon
password
Property
Aug 25, 2023 05:15 PM
URL
1. 一般旋转曲面
1.1 一般的数学定义
如图所示,我们说
- 绕轴旋轴的曲线称作 母线
- 中间这个轴叫做 旋旋轴
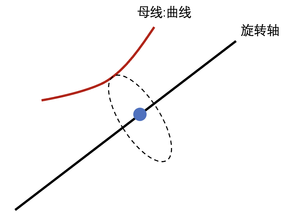
母线绕轴旋转一周会得到一个旋转曲面,类似于下面这样的图.
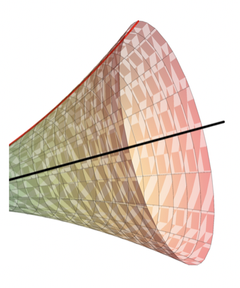
1.2 数学求解
我们知道空间直角坐标系中 曲线 是由于 面和面 相交得到的
所以我们可以用连立两个曲面的方程,就能得到曲线的表达式了,如下
这个旋转轴无法就是一个直线,我们同样可以定义一个一般直线:
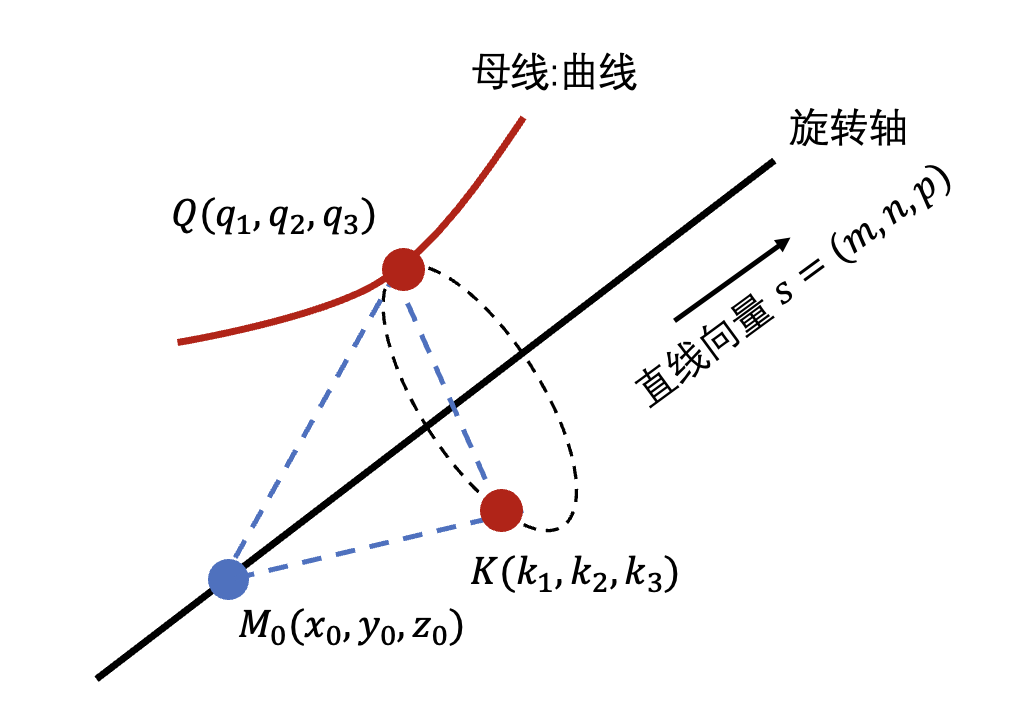
- 这里的 是曲线上的任意一点,曲线从这个点开始绕旋转轴旋转.
- 这里 是直线点法式的初始点, 是直线的向量
- 我们要求曲面的方程实际上就是从曲面上任意找一点 然后建立方程求解即可
从图中我们可以看到两个条件
( 1 )
( 2 )
基于这两点我们就能建立两个方程:
然后再和
连立,消去 就能得到我们想要的了
2. 编程实现
2.1 总代码
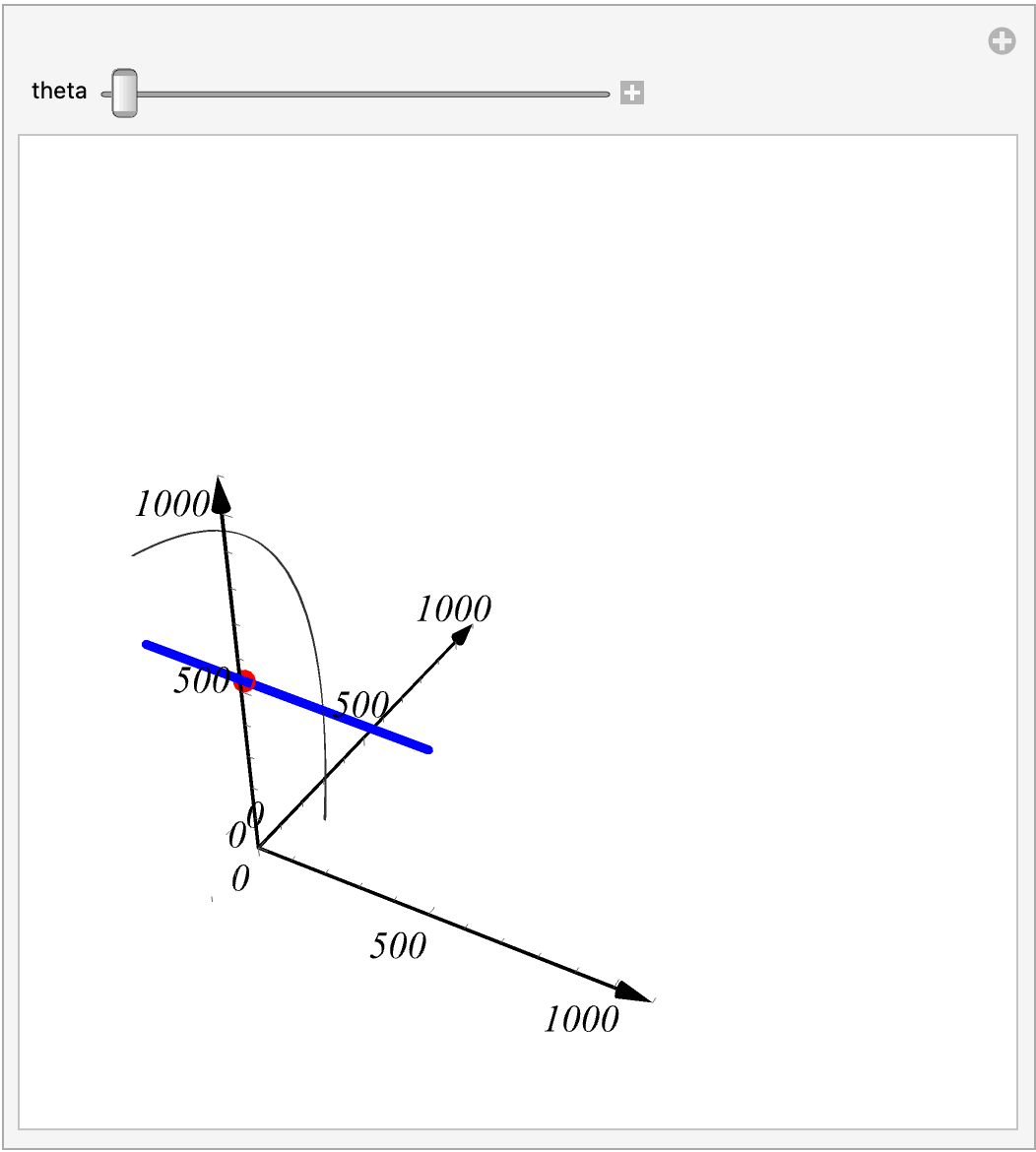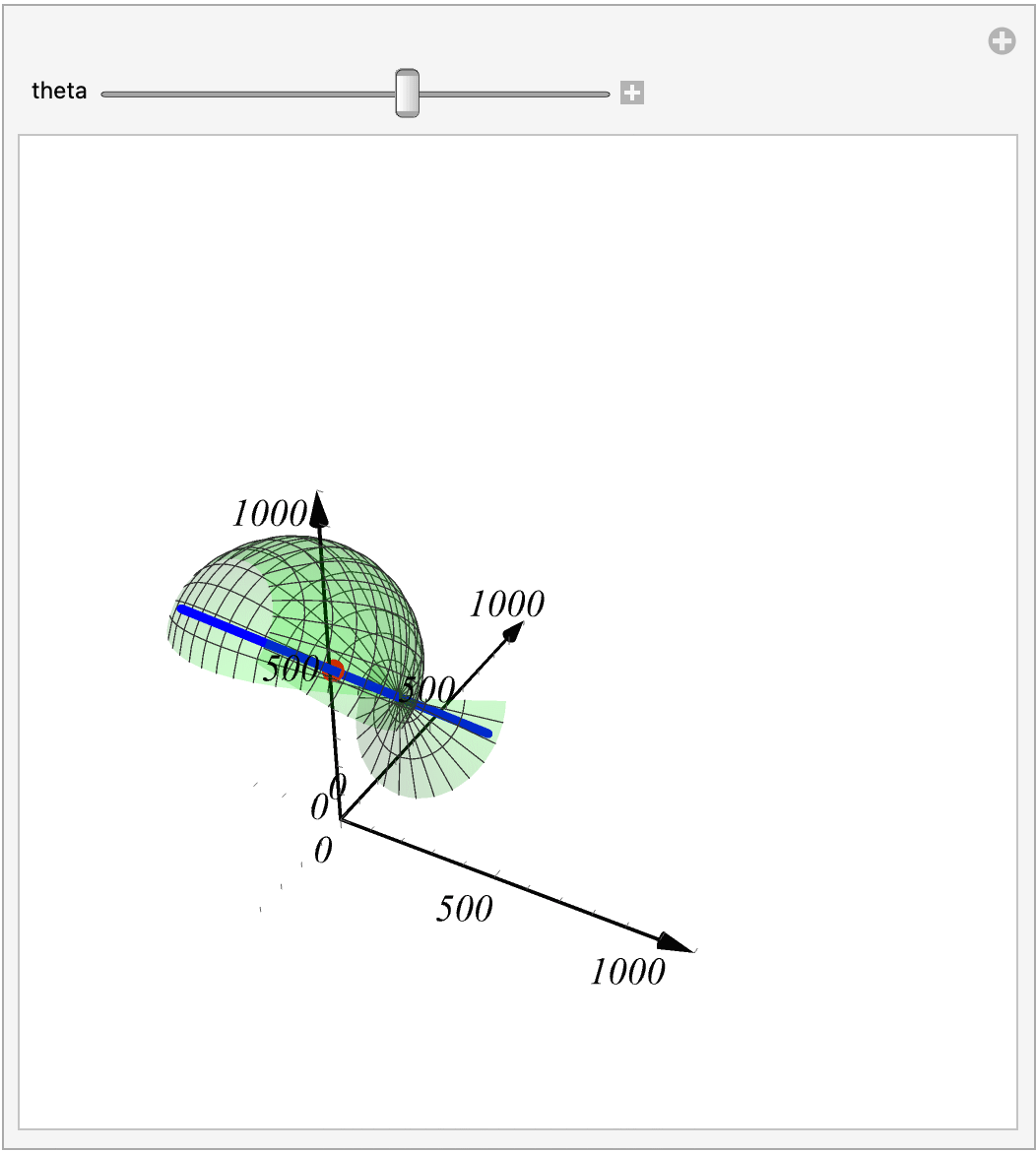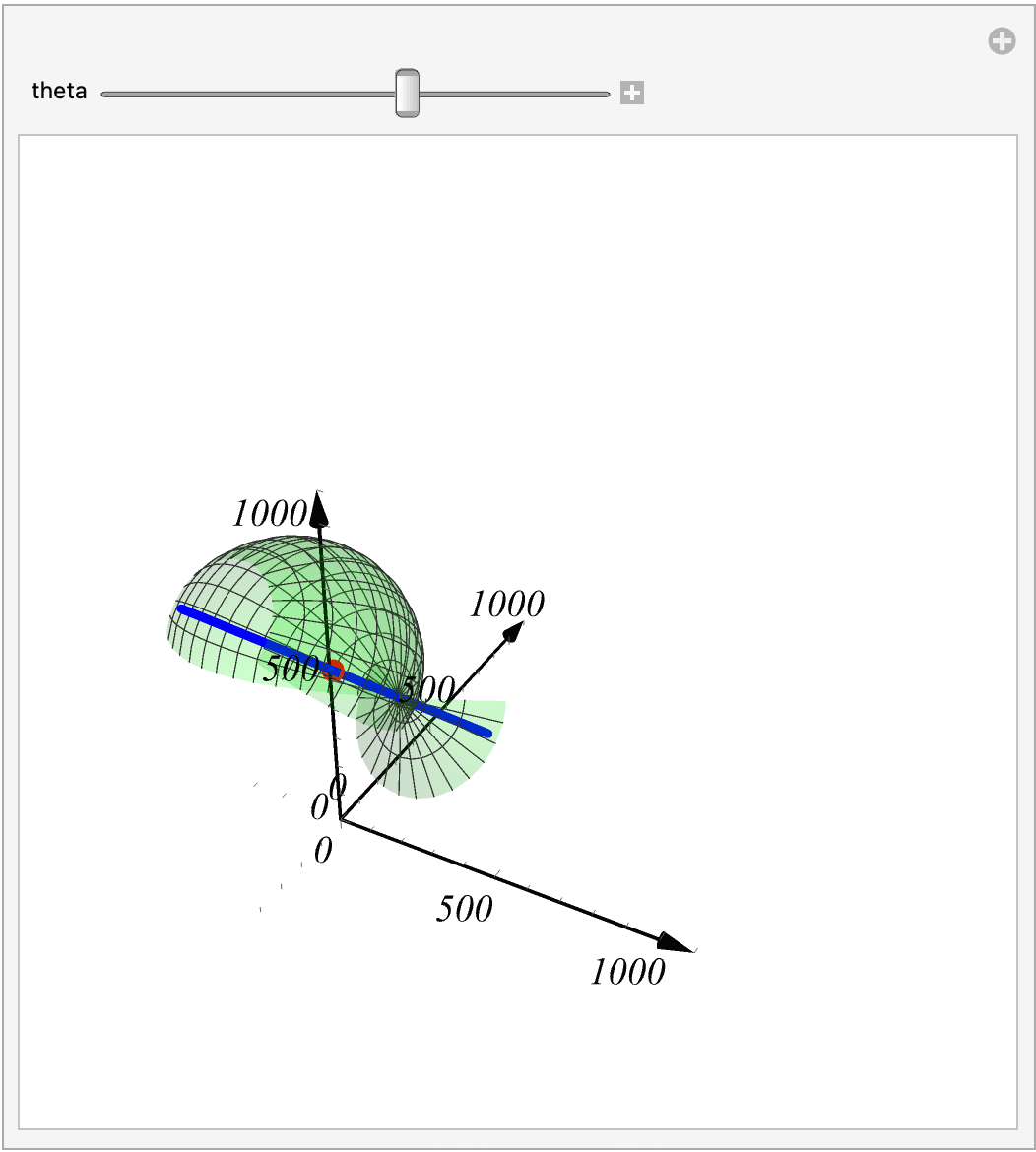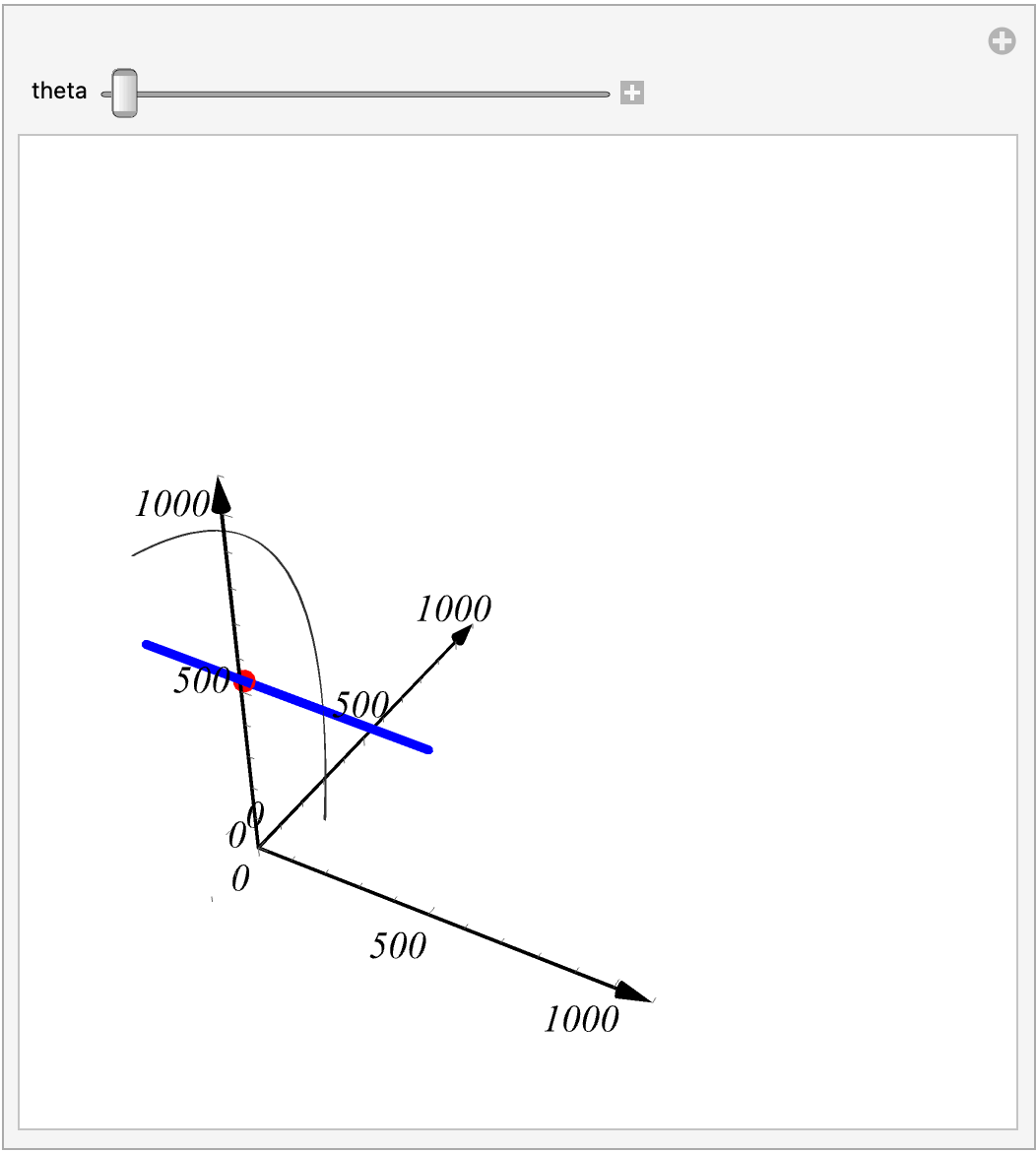
2.2 代码的剖析
- 作者:NotionNext
- 链接:https://tangly1024.com/article/wolfram-sz2
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。




